Chamber to barrel ratio
The Chamber to Barrel ratio, or C:B ratio, is the ratio of the volume of the chamber and barrel;
| (Volume Chamber) | ||
| C:B Ratio | = | |
| (Volume Barrel) |
The volume of a cylindrical shape can be calculated with the following formula, where "r" stands for the radius of the inner diameter of the pipe and "h" stands for height, which is the same as length:
- V = π x r² x h
Make sure you use the same units for both the radius and length of both your barrel and your chamber. Note that elbows or other parts also count as part of the volume. If you want to be even more precise in calculating the volume of some shape, you could water measure it.
The ratio determines how much of the available energy is transferred to the projectile. A good C:B ratio is a major factor in combustion cannon performance. The goal of an optimal ratio is to have the barrel end at the exact point where the projectile stops accelerating.
Higher ratio (shorter barrel) cannons are louder since significant pressure is still present in the chamber when the projectile exits the barrel. The high pressure results in a significantly louder "bang" from the gun, similar to the loud pop from the opening of a pressurized bottle of Champagne. Too low a ratio will also hurt performance since a vacuum is formed behind the projectile if it travels too far or if the combustion gases cool significantly before the projectile exits the barrel. In extreme cases of low C:B ratio the projectile may even be sucked back into the chamber. [1]
Experiments have shown that a C:B ratio of about 0.6-0.8:1 is the most efficient for a given chamber using potatoes as projectiles. The ratio will vary somewhat depending on the weight, friction, diameter and blow by of a particular projectile, as well as the fuel, ignition type and perhaps other variables. In most cases though, the optimal C:B is expected to be in the 0.6 to 0.8 range.
C:B Ratio Studies
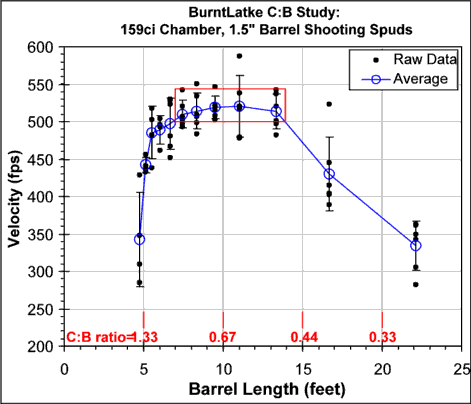
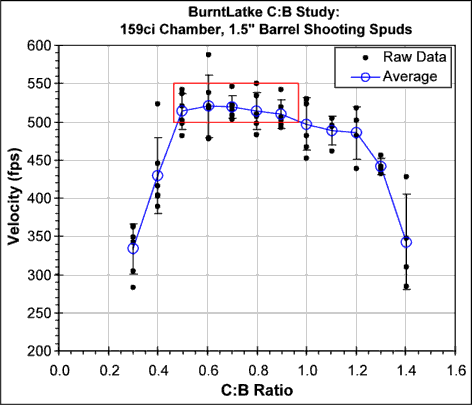
The actual affect of changing the C:B ratio on the muzzle velocity for a typical gun is shown in the two graphs below (data from BurntLatke.) The first graph gives the muzzle velocity as a function of barrel length, the second graph the barrel length axis has been converted to C:B ratios.
As you can see from the graphs, this particular chamber / barrel / fuel / ammo combination gives the greatest muzzle velocity (521 FPS) with an 11 foot long barrel. The C:B for this barrel is 0.60.
The two graphs also indicate another key characteristic of the affect of the C:B ratio on the performance of a combustion spudgun. The muzzle velocity is fairly insensitive to small changes in the C:B near the optimal C:B. For this gun, removing 3.6 feet from the barrel, 1/3 of the barrels total length, to a C:B=0.90 only dropped the muzzle velocity by 10 FPS. That is less than a 2% change in the muzzle velocity for a 33% shorter barrel. Similarly, increasing the barrel from 11' to 13.3' (C:B=0.5) only decreased the muzzle velocity from 521 FPS to 514 FPS. For both the shorter and longer barrels the decrease in the average muzzle velocity is less than the ~5% shot-to-shot variability of this gun and ammo.
The combination of a broad and flat velocity versus C:B (or barrel length) curve and the relatively high shot-to-shot variability for shooting spuds, suggests that the C:B ratio does not have to be all that close to the optimal to get essentially optimal performance from a gun. For the gun used to generate the graphs above, shortening the barrel by 1/3 from the optimal length had essentially no affect on the performance of the gun. The red boxes on the two graphs indicate the range of barrel lengths and C:B ratios for which the muzzle velocity is within 5% of the optimal.
If you can tolerate a slightly larger performance drop of say 10%, then the C:B can range from 0.5 to ~1.2.
Note that this affect is only true over this 0.5~1.2 C:B ratio range. Outside of this range the muzzle velocity drops off very rapidly. For this gun / ammo / fuel combination, a C:B of 0.3 drops the velocity from 521 FPS to 330 FPS. A C:B of 1.4 drops the velocity from 521 FPS to 340 FPS.
A statistical analysis of this set of velocity versus barrel length data indicates that there is no statistically significant difference for C:Bs in the range of 0.5 to 1.2. (Student's T-Test, unequal variance, two tailed, P<0.05). Note that this does not mean there is no difference over this range of C:Bs. Instead, it says this study was unable to measure the difference. It appears that the relatively high shot-to-shot variability is obscuring the fine details of the relationship between barrel length (or C:B) and muzzle velocity.
One might ask the question "Can't the optimal C:B ratio be easily calculated"? A simple minded approach would be to calculate the barrel volume at which the pressure in the chamber is equal to atmospheric pressure plus the force required to overcome dynamic friction between the spud and the barrel. If we assume atmospheric pressure is 15 PSIa (absolute) and that a typical spud in a 2" barrel has 5 PSI of friction then the spud will continue to accelerate until the chamber pressure has dropped below 15+5=20 PSIa. The combustion of propane in air generates about 135 PSIa of pressure. The ratio of the combustion pressure to the minimal pressure, 135/20=6.75, is the ratio of the chamber to the chamber plus the optimal barrel. Therefore, this simple minded approach says that the optimal C:B should be 1/(6.75-1)=0.17. This C:B would give a barrel nearly five times longer than the observed optimal barrels. Indeed, according to the BurntLatke studies, a spud won't even exit the barrel at a C:B this low. Clearly, there are more complex factors affecting the optimal C:B ratio of a combustion spudgun. Suggestively, the optimal C:B ratio for pneumatic guns, as predicted by GGDT are in the vicinity of 0.2~0.3, close to the simple minded calculation outlined above.
Theories on the C:B Ratio
Several theories exist explaining the optimal barrel for a particular chamber. A brief summary of three are given below.
1. A chamber volume that exceeds the optimal value for efficiency will increase performance since more energy is available within the chamber. This theory is based on the "fast combustion model" in which the fuel burns quickly relative to the movement of the projectile. The pressure rises to it's maximum before the projectile has moved a significant distance down the barrel. When designing a launcher using this theory, a larger chamber will produce better performance.
2. The most efficient ratio will usually also produce the highest performance. (Internal combustion engines fall into this category, the most efficient engine speed usually also produces the most power.) This theory is based on a "slow combustion model". A chamber that is too large takes longer to burn the fuel, the pressure rises more slowly, the projectile starts to move through the barrel at lower pressures and the exits before maximum pressure is reached. This results in lower projectile speed. This model is similar to a slow opening pneumatic valve. If the chamber is grossly oversized, combustion may not complete until after the projectile leaves the barrel, further reducing performance. When designing a launcher, the chamber and barrel should be matched to each other for optimal performance. A ratio anywhere between 0.5:1 and 1:1 will be ideal under most circumstances.
3. A hybrid "slow / fast combustion model". In the first two models the combustion process is considered to be independent of the projectile's movement through the barrel. In the "hybrid" model the movement of the projectile affects the burning process. In particular, movement of the projectile allows the gases in the chamber to move, this causes turbulence which in turn increases the rate at which the fuel burns. This model may explain the broad flat velocity versus C:B (or barrel length) graphs. A slow moving projectile has a slow fuel burn speed, a fast moving projectile gives a faster burn speed. The slow moving projectile takes longer to exit the barrel and there is more time for the fuel to burn. A fast moving projectile takes less time to exit but it's movement makes the fuel burn faster.
Interestingly, gasoline engines display this characteristic "projectile speed" versus fuel burn speed relationship. The time available for the fuel-air mixture to burn in an engine is dependent on the RPMs the engine is running at. At high RPMs there is less time for the fuel to burn compared to low RPMs. (In most simple gasoline engines the fuel injected per combustion cycle is independent of the engines RPM.) Studies of the fuel burn rate as a function of the engine RPMs indicate that the fuel burns faster at high RPMs than at low and that combustion occurs thoughout most of the power stroke.
Very little hard data is available to help differentiate between these and other possible models.
Summary
C:B ratios are good for predicting what barrel will yield the highest performance given a fixed chamber volume. In addition, the C:B ratio will be indicative of the noise output of the gun. With sufficient data, the C:B ratio will also be useful for determining what chamber volume will deliver optimal performance given a fixed barrel. However, a single highly precise value should not be interpreted as the optimal value for all cannons.
Other Aspects of C:B Ratios
Burst disks can be used to increase the performance of high ratio (short barrel) cannons, since they let higher pressure build up before the projectile starts to move. They will not increase the performance significantly in near optimal cannons. Source
Multiple spark gaps, spark position and a Chamber fan may also affect the optimal C:B for a particular cannon. Currently there is relatively little reliable data on the affect of these parameters on the optimal C:B ratio.
The C:B ratio plays a much smaller role in the design of pneumatic cannons since factors like chamber charge pressure and valve performance play a greater role in determining overall performance. It is advisable to use GGDT to determine the best design for pneumatic cannons.